Internals¶

To start describing our internals, let us make it clear on our dependency structure:

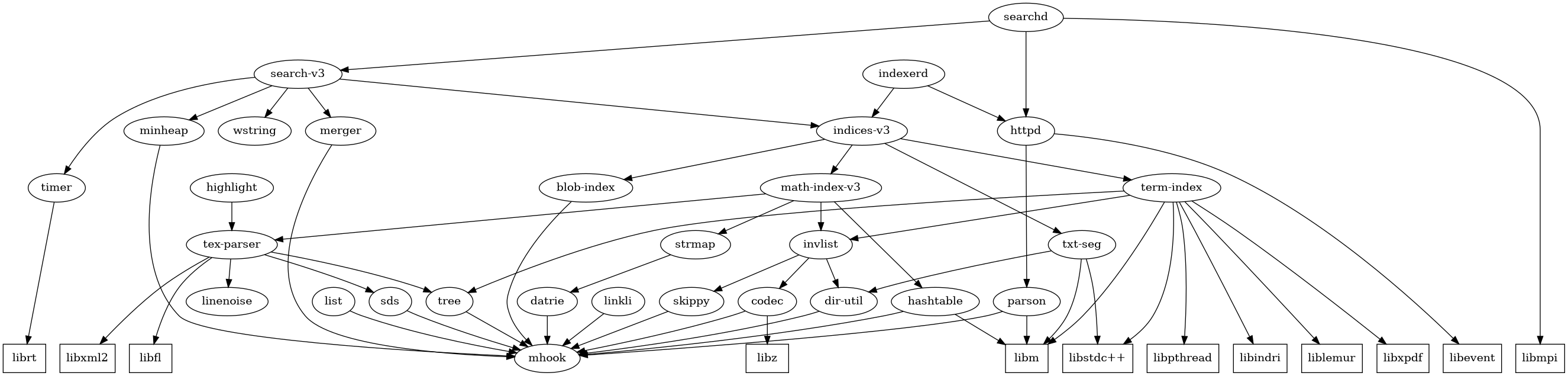
../../_images/dep.png

(Boxes are external dependencies, circles are internal modules)

To generate this module dependency graph, issue commands below at the project top directory:

$ mkdir -p tmp
$ python3 proj-dep.py --targets > targets.mk
$ python3 proj-dep.py --dot > tmp/dep.dot
$ dot -Tpng tmp/dep.dot > tmp/dep.png

Now, we will tell the story by walking through the key modules here.

TeX Parser¶

TeX parser converts TeX to Operator Tree (or OPT) and leaf-root paths. There are many details involved, among them

Each node in OPT will be assigned a ID in a way that leaf nodes always occupy lower space
Each node in OPT will save its position [start, end] information from original TeX string
Fingerprint (or fp) (the symbol hash digested from 4 nodes on top of a node) is generated for each leaf-root path
A subtree Hash is generated for each subtree
A pathID and a leafID (starting from 1) are generated for each path, initially they are the same
Max pathID/leafID is also the maximum number of leaf-root paths here, they are no greater than MAX_SUBPATH_ID = 64
Any nil node will be pruned
Each meaningful internal node (non-meaningful are tokens like T_BASE, T_SUBSCRIPT, T_SUPSCRIPT or T_NIL) gets assigned a pathID which is the pathID from one of its descendant leaf child. Also, non-meaningful nodes are not counted when generating fingerprint.
A rank number will be assigned to its children if a node is non-communitive node (such as fraction operator)

The following is an example output for expression $a + a + b/c=$

(notice the RHS has nothing so it will reduce into nil)

Operator tree:
     └──(equal) #6, token=GTLS, subtr_hash=`28392', pos=[0, 15].                                                               
           └──(plus) #7, token=ADD, subtr_hash=`23672', pos=[0, 15].                                                           
                 │──(pos) #8, token=SIGN, subtr_hash=`26696', pos=[0, 1].                                                      
                 │     └──(hanger) #9, token=HANGER, subtr_hash=`4808', pos=[0, 1].                                            
                 │           └──(base) #10, token=BASE, subtr_hash=`1160', pos=[0, 1].                                         
                 │                 └──[normal`a'] #1, token=VAR, subtr_hash=`a', pos=[0, 1].                                   
                 │──(pos) #11, token=SIGN, subtr_hash=`26696', pos=[4, 5].                                                     
                 │     └──(hanger) #12, token=HANGER, subtr_hash=`4808', pos=[4, 5].                                           
                 │           └──(base) #13, token=BASE, subtr_hash=`1160', pos=[4, 5].                                         
                 │                 └──[normal`a'] #2, token=VAR, subtr_hash=`a', pos=[4, 5].                                   
                 │──(pos) #14, token=SIGN, subtr_hash=`25732', pos=[8, 11].                                                    
                 │     └──(frac) #15, token=FRAC, subtr_hash=`57044', pos=[8, 11].                                             
                 │           │──#1(hanger) #16, token=HANGER, subtr_hash=`4820', pos=[8, 9].                                   
                 │           │     └──(base) #17, token=BASE, subtr_hash=`1164', pos=[8, 9].                                   
                 │           │           └──[normal`b'] #3, token=VAR, subtr_hash=`b', pos=[8, 9].                             
                 │           └──#2(hanger) #18, token=HANGER, subtr_hash=`4832', pos=[10, 11].                                 
                 │                 └──(base) #19, token=BASE, subtr_hash=`1168', pos=[10, 11].                                 
                 │                       └──[normal`c'] #4, token=VAR, subtr_hash=`c', pos=[10, 11].                           
                 └──(pos) #20, token=SIGN, subtr_hash=`26876', pos=[14, 15].                                                   
                       └──(hanger) #21, token=HANGER, subtr_hash=`4844', pos=[14, 15].                                         
                             └──(base) #22, token=BASE, subtr_hash=`1172', pos=[14, 15].                                       
                                   └──[normal`d'] #5, token=VAR, subtr_hash=`d', pos=[14, 15].

4 leaf-root paths:
- [path#1, leaf#1] normal`a': VAR(#1)/BASE(#10)/HANGER(#9)/SIGN(#8)/ADD(#7)/GTLS(#6) (fp 3552)                                 
- [path#2, leaf#2] normal`a': VAR(#2)/BASE(#13)/HANGER(#12)/SIGN(#11)/ADD(#7)/GTLS(#6) (fp 3552)                               
- [path#3, leaf#3] normal`b': VAR(#3)/BASE(#17)/HANGER(#16)/rank1(#0)/FRAC(#15)/SIGN(#14)/ADD(#7)/GTLS(#6) (fp 0552)           
- [path#4, leaf#4] normal`c': VAR(#4)/BASE(#19)/HANGER(#18)/rank2(#0)/FRAC(#15)/SIGN(#14)/ADD(#7)/GTLS(#6) (fp 0552)           
- [path#5, leaf#5] normal`d': VAR(#5)/BASE(#22)/HANGER(#21)/SIGN(#20)/ADD(#7)/GTLS(#6) (fp 3552) 

You can find the interface tex_parse() at tex-parser/tex-parser.h

struct tex_parse_ret {
    uint32_t         code;
    char             msg[MAX_PARSER_ERR_STR];
    struct subpaths  lrpaths;
    void            *operator_tree;
};

struct tex_parse_ret tex_parse(const char *); 

(the word subpath refers to a full length leaf-root path or any paritial path)

Math Index¶

The math_index_add() interface at math-index-v3/math-index.h

size_t math_index_add(math_index_t, doc_id_t docID, exp_id_t expID, struct subpaths);

will take a specified docID, expID and parser generated leaf-root paths from a math formula, to generate a subpath set which consists of all possible [1] leaf-to-internal-node subpaths (or prefix paths) from that subpath set (exclude those rooted at a RANK node), and group them by their path token sequence. Multiple prefix paths falling into same group are called to contain duplicates.

Within each group, if a subgroup of paths have the same root-end nodeID, they are called a sector tree because they must have identical length and the same token sequence. However, the leaf symbols in a sector tree may vary, alternatively, we say they may contain different splits. The size of a sector tree or a split is referred as width.

Math indexer will ensure that the number of generated sector trees is no greater than MAX_SUBPATHS and it will remove those excessive paths starting from the longest.

An example subpath set generated from above example leaf-root paths:

subpath set (size=13)
[  0] prefix/VAR/BASE (4 duplicates: r10~l1 r13~l2 r17~l3 r19~l4 r22~l5 )
         qnode#10/1-0003{ normal`a'/1 0x1 } 
         qnode#13/1-0003{ normal`a'/1 0x2 } 
         qnode#17/1-0003{ normal`b'/1 0x4 } 
         qnode#19/1-0003{ normal`c'/1 0x8 } 
         qnode#22/1-0003{ normal`d'/1 0x10 } 
[  1] prefix/VAR/BASE/HANGER (4 duplicates: r9~l1 r12~l2 r16~l3 r18~l4 r21~l5 )
         qnode#9/1-0035{ normal`a'/1 0x1 } 
         qnode#12/1-0035{ normal`a'/1 0x2 } 
         qnode#16/1-0030{ normal`b'/1 0x4 } 
         qnode#18/1-0030{ normal`c'/1 0x8 } 
         qnode#21/1-0035{ normal`d'/1 0x10 } 
[  2] prefix/VAR/BASE/HANGER/SIGN (2 duplicates: r8~l1 r11~l2 r20~l5 )
         qnode#8/1-0355{ normal`a'/1 0x1 } 
         qnode#11/1-0355{ normal`a'/1 0x2 } 
         qnode#20/1-0355{ normal`d'/1 0x10 } 
[  3] prefix/VAR/BASE/HANGER/SIGN/ADD (2 duplicates: r7~l1 r7~l2 r7~l5 )
         qnode#7/3-3552{ normal`a'/2 0x3 normal`d'/1 0x10 } 
[  4] prefix/VAR/BASE/HANGER/rank1/FRAC (0 duplicates: r15~l3 )
         qnode#15/1-3055{ normal`b'/1 0x4 } 
[  5] prefix/VAR/BASE/HANGER/rank2/FRAC (0 duplicates: r15~l4 )
         qnode#15/1-3055{ normal`c'/1 0x8 } 
[  6] prefix/VAR/BASE/HANGER/SIGN/ADD/GTLS (2 duplicates: r6~l1 r6~l2 r6~l5 )
         qnode#6/3-3552{ normal`a'/2 0x3 normal`d'/1 0x10 } 
[  7] prefix/VAR/BASE/HANGER/rank1/FRAC/SIGN (0 duplicates: r14~l3 )
         qnode#14/1-0552{ normal`b'/1 0x4 } 
[  8] prefix/VAR/BASE/HANGER/rank2/FRAC/SIGN (0 duplicates: r14~l4 )
         qnode#14/1-0552{ normal`c'/1 0x8 } 
[  9] prefix/VAR/BASE/HANGER/rank1/FRAC/SIGN/ADD (0 duplicates: r7~l3 )
         qnode#7/1-0552{ normal`b'/1 0x4 } 
[ 10] prefix/VAR/BASE/HANGER/rank2/FRAC/SIGN/ADD (0 duplicates: r7~l4 )
         qnode#7/1-0552{ normal`c'/1 0x8 } 
[ 11] prefix/VAR/BASE/HANGER/rank1/FRAC/SIGN/ADD/GTLS (0 duplicates: r6~l3 )
         qnode#6/1-0552{ normal`b'/1 0x4 } 
[ 12] prefix/VAR/BASE/HANGER/rank2/FRAC/SIGN/ADD/GTLS (0 duplicates: r6~l4 )
         qnode#6/1-0552{ normal`c'/1 0x8 }

For instance, the sixth item of subpath set has 3 prefix paths of token

/VAR/BASE/HANGER/SIGN/ADD/GTLS

and there is one sector tree rooted at node#6 with width=3:

[  6] prefix/VAR/BASE/HANGER/SIGN/ADD/GTLS (2 duplicates: r6~l1 r6~l2 r6~l5 )
         qnode#6/3-3552{ normal`a'/2 0x3 normal`d'/1 0x10 } 

where 3552 is fingerprint (or ophash) of that sector tree, and it contains two splits: Those have leaf a with width=2, and a path with leaf d has width=1. Here 0x3 and 0x10 are 64-bit mask to represent corresponding leaf/leaves.

A sector tree is the primary index item in math inverted list (they are mapped by their token sequences), it contains minimal information to test structure differences between two operator trees in a efficient way.

And the splits from a sector tree is indexed in a separate list called symbinfo list in which symbol information are stored to test symbolic similarity between math formulas to break tie similarity scores if their structures are not dramatically different.

Here is the C code snippet defining the math inverted list structure and its corresponding symbinfo list:

/* math inverted list items */
struct math_invlist_item {
	/* 8-byte global key */
	uint32_t docID; /* 4 bytes */
	union {
		uint32_t secID;
		struct {
			uint16_t sect_root;
			uint16_t expID;
		};
	}; /* 4 bytes */

	uint8_t  sect_width;
	uint8_t  orig_width;
	/* padding 16 bits here */
	uint32_t symbinfo_offset; /* pointing to symbinfo file offset */
	/* 4 bytes */
}; /* 4 x 4 = 16 bytes in total */

#define MAX_INDEX_EXP_SYMBOL_SPLITS 8

struct symbsplt {
	uint16_t symbol;
	uint8_t  splt_w;
};

struct symbinfo {
	uint32_t ophash:24;
	uint32_t n_splits:8;

	struct symbsplt split[MAX_INDEX_EXP_SYMBOL_SPLITS];
};

[1]: Note the huge number of prefix paths can be a great overhead, so they are usually statically pruned in practice (if search does not require to be rank-safe). The criteria is to test if a path root-end has a width less than “root_width times MATH_INDEX_STATIC_PRUNING_FACTOR”.

Search¶

The entrypoint for search functionality is indices_run_query() function at search-v3/search.dt.c:

typedef struct {
    uint32_t docN;
    uint32_t avgDocLen;
    uint32_t pathN;
    uint32_t doc_freq[MAX_MERGE_SET_SZ];
} indices_run_sync_t;

priority_Q
indices_run_query(struct indices* indices, struct query* qry, indices_run_sync_t *run_sync);

where priority_Q is a minheap data structure for storing dynamic top-K search results, and run_sync is the index statistics possibly added up from sub-indexes.

indices_run_query() function will initialize a term_qry structure for each text term and a level-2 inverted lists for each math keyword.

The term_qry structure

struct term_qry {
    char *kw_str;   
    uint32_t term_id;
    uint32_t df; /* document frequency (set to doc_freq[i] under run_sync) */
    float qf; /* query term frequency */
    float idf; /* BM25 idf */
    float upp; /* BM25 tf-idf upperbound score */
}; 

is initialized according to Okapi BM25 scoring (free parameters $k_1 \in [1.2, 2.0]$ and $0 \le b \le 1$), $$ \newcommand{\tf}{\operatorname{TF}} \tf(q, d) = \dfrac{\tf \times (k_1 + 1)}{ \tf + k_1 (1 - b + b \cdot \operatorname{docLen} / \operatorname{avgDocLen} )} \le \dfrac{k_1 + 1}{1 + k_1 (b/\operatorname{avgDocLen})} $$ and $$ \newcommand{\df}{\operatorname{DF}} \operatorname{IDF}(q) =\log \dfrac{\operatorname{docN} - \df + 0.5}{\df + 0.5} $$

On the other hand, math keyword will generate a level-2 inverted list in which path frequency and pathN (total number of paths) are also synchronized to run_sync.

A math keyword upperbound is calculated based on “SF-IDF” (Significance-factor IDF), specifically, SF is significance score and IDF here is actually sum-of-logs from inverted path frequency ($ \log \frac N {\operatorname{PF}} $ or IPF). The upperbound score for a level-2 math keyword is based on math similarity scoring scheme: $$ \operatorname{SF}(q, d) = \dfrac{1}{1+ (1- \operatorname{symSim})^2} ((1- \eta) + \eta \dfrac{1}{\log(1 + \operatorname{formulaLen})}) $$ and $$ \operatorname{IDF}(q) = \sum_p \operatorname{IPF}_p $$

The math keyword with maximum upperbound score will associate a MATH_REWARD_WEIGHT and other math keyword will associate a MATH_PENALTY_WEIGHT weight.

After preparing keywords, all inverted list iterators are generated and they are inserted into a max-score merger. The order of merge lists are:

[0] high upp term keyword
...
[k] low upp term keyword
[k+1] high upp math keyword
...
[n] low upp math keyword

Internals¶

TeX Parser¶

Math Index¶

Search¶

Further Reading¶